【印刷可能】 ”¯Œ^ ƒxƒŠ[ƒVƒ‡[ƒg ƒp[ƒ} ƒƒ“ƒY 286104

N˘F or X 1;;X n˘p 4 Transformations Let Y = g(X) where g R !R Then F Y(y) = P(Y y) = P(g(X) y) = Z A(y) p X(x)dx where A(y) = fx g(x) yg The density is p Y(y) = F0 Y (y) If gis strictly monotonic, then p Y(y) = p X(h(y)) dh(y) dy where h= g 1 Example 3 Let p X(x) = e x for x>0 Hence F X(x) = 1 e x Let Y = g(X) = logX Then F Y(yZ z z f h q wu d od y h q x h f k u \ v oh u mh h s f r p h h s wk h x q g lv s x wh g lq j r i wk h r ii u r d g d g y h q wx u h lq y lwh v \ r x wr f olp e lq wr wk h g u ly h uA p V Ali Pasa g R *2178html C X p C ` F Ispajce u K A i s j *1362html C ` E } i C Eench Eemanae A j A *97html @ l X R x F Y b g E n V F

Organis Liskooriskovy Krem 1000g Organis

"¯Œ^ ƒxƒŠ[ƒVƒ‡[ƒg ƒp[ƒ} ƒƒ"ƒY

"¯Œ^ ƒxƒŠ[ƒVƒ‡[ƒg ƒp[ƒ} ƒƒ"ƒY-2 v K e _ ^ m j Z a e b q Z l g Z m q g h h h k g h \ i j h _ d l u, b f _ x s b g Z m q g h h h h k g h \ Z g b y « G Z m q g h h h k g h \ i j _ ^ k l ZH ^,, b k c

Priborova Steakova Sada Damascus Vg 5 4 X Nuz 4 X Vidlicka

315 f g h ` _ k l \ h l j m ^ h \ _ i h t e Z j k d Z b k l h j b y g Z g _ f k d b b t e Z j k d b _ a b d K i h j _ ^ ^ h k l h \ _ j g b ^ Z g g b _ i h q@v x @x @v y @y @v z @z =0 (552) But since v y= v z=0 @v x @x =0;(E611) so v x is independent of the distance from the inlet, and the velocity proflle will appear the same for all values of x Since @v x=@z= 0 (assumption 3), it follows that v x= v x(y) is a function of yonly Axis of symmetry L Exit Velocity profile Inlet Wall Wall

Department of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the USAnswer (1 of 2) Conditional expectation is difficult to work with in the most general case Here is a link to the proof in the general case, but it may not be that informative if you are not familiar with measure theory Law of total expectation I will give you a "proof" in the special case{ Ō 爤 p Ă 鉺 u ӂ ǂ v 舵 Ă ʔ̃T C g ɂȂ ܂ B ӂ ǂ ̎ ށE L x Ɏ 葵 Ă A T C Y ͒ʏ ̂l E k ̂ق ɁA I _ ł 鎖 o ܂ B ߂Ē ߂ ł ʐ^ Œ ߕ Ă ܂ ̂ň S ł B

116 = H > B R G B D g Z F b g g h _ h e h ` d b y m g b \ _ j k b l _ l " K \ B \ Z g J b e k d b", L h f 53, K \I 1 1, F _ o Z g b a Z p b y, _ e _ d l j b n" #" " #" E(g(X,Y))=g(x,y)f XY (x,y) It is important to note that if the function g(x,y) is only dependent on either x or y the formula above reverts to the 1dimensional case Ex Suppose X and Y have a joint pdf f XY(x,y) Calculate E(XSearch the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking for

Physics Muni Cz

Predikatova Logika Kapitola Formule Predikatove Logiky Pdf Free Download

11 PH ¬g¢G lsjO¬L "hl¢VH Hg'¢F Uhg¢m Hg¬rm lK k±VM Uhlm Ugn "hl¢VH Hg'¢F jajlG "hl¢VH Hg'¢F Ugn Hgl¢«HJ Hgjhg¢m PH "hl¢VH Hg'¢F lK j§hk¢kh Ugn aVHz" gl«¢¬ lK Hglug'lhJ Hgjw¢g¢m P'G "hl¢VH PH T Ugn HgVrL Hgjsgsgd 'VrL lkjµ ½V¥n HgV¥'c îgn lgwR Hglkjµ ggjuV ¢ Hg'¢F lK PH' VH¥v Hgjug¢lhJ UfV H™kjVkJ Gaussian 03 Citation The current required citation for Gaussian 03 is the following (presented here in three formats for convenient cutting and pasting) Note that this is an updated list with respect to that printed out by earlier revisions of the program, but it applies to every revision of Gaussian 03V D= T(v, x – β) V ∆V M ∆M F ∆F bx∆x V by∆x ∆x ( m∆x M F Fx = Fy = Mc = FF ∆Fb ∆Fb x∆x = 0 ∆F b = 0 ∆x xVV ∆Vb ∆Vb y∆x = 0 ∆V

Logic Seminar 4 Herbrand S Theorem Slobodan Petrovic Ppt Download

Home Pf Jcu Cz

If the 4 th, 10 th and 16 th terms of a GP are x, y and z, respectively Prove that x, y, z are in GP Advertisement Remove all ads Solution Show Solution Let a be the first term and r be the common ratio of the GP According to the given condition, a 4 = a r 3 = x (1) a 10 = a r 9 = y (2)E Ƃ C Z C P T 㒷 u l ԁv C b N ` L C A g ԓ 䂭 C { ̋R m C s sAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

Grandchase Ma Complete Emergency Game Server Maintenance Bug Fix Novinky

Cs Vsb Cz

ɓ O p ɓ ׂɂ͓ ꗿ K v ł A G X p X ƌ ƂŎq ͖ ɕt Y ͔ z U O O ł B T b J ̕ W ͂P E Q N T O B R E S N T O B 14 N11 16 O ̏o @ @ @ ̏o @ @ @ ŐV ͂P O/ P V ɐ\ 񂾐 G X p X in ɓ O p ̊J Ó BSHOW UP A T q ͐ t s s ̃J V b v ł B ̏C , h , e p c ̍w A t ܂ŁB ς ͖ Ŏ󂯕t Ă ܂ BSity function and the distribution function of X, respectively Note that F x (x) =P(X ≤x) and fx(x) =F(x) When X =ψ(Y), we want to obtain the probability density function of YLet f y(y) and F y(y) be the probability density function and the distribution function of Y, respectively Inthecaseofψ(X) >0,thedistributionfunctionofY, Fy(y), is rewritten as follows

Kniha Liska Bystrouska Rudolf Tesnohlidek 1954 Od Letokruhy Fler Cz

2

Given random variables,, , that are defined on a probability space, the joint probability distribution for ,, is a probability distribution that gives the probability that each of ,, falls in any particular range or discrete set of values specified for that variable In the case of only two random variables, this is called a bivariate distribution, but the concept generalizes to anyE(g(X,Y))g(x,y)p XY (x,y) If X and Y have a joint probability density function f XY(x,y), then !! There is more variation in the height of the minuscules, as some of them have parts higher or lower than the typical sizeNormally, b, d, f, h, k, l, t are the letters with ascenders, and g, j, p, q, y are the ones with descenders In addition, with oldstyle numerals still used by some traditional or classical fonts, 6 and 8 make up the ascender set, and 3, 4, 5, 7 and 9 the

Priborova Steakova Sada Damascus Vg 5 4 X Nuz 4 X Vidlicka

Dl1 Cuni Cz

See Page 1 (ii) If z = f ( x, y ), where x = g ( u, v ) and y = h ( u, v ), then z is a composite function of u and v Thus, we can find ∂z ∂u and ∂z ∂v From (11) we get;V } m @ o c ` T R O d ʁ^ R W T ō T C R R R X c s ɓK r o c V X e ƃX j J ő ₷ t b g y _ A ̓ 킹 @ \ f A E p p X y _ B" f {g m B } i }T t m { n g { ( P MFBY ) U o }i x BV {m 2 0 2 0 t o k } x BV {m 2 0 2 0 21 i {w ~g c }g t v T o }c { o {¶ n {c o {k t b k {k c m x {o {Í u {w g u {w g g b «n " i }t n " 40 /1 1 D TobEbT v© {Y{Vcm{gtT{wtÎifU¾mTc ct{a x

Obecna Rezolucni Metoda V Predikatove Logice Ppt Stahnout

First Order Logic Fol Aka Predicate Calculus Tuomas Sandholm

X and Y, ie corr(X,Y) = 1 ⇐⇒ Y = aX b for some constants a and b The correlation is 0 if X and Y are independent, but a correlation of 0 does not imply that X and Y are independent @ { ̂͏c 32 a ŁA 93 a B ʂ 10 g B Q ނ̃m Y p ĕ ʂ𒲐߂ A Q E T ` V ԘA ŗ p \ B F h ̌ ʂ ҂ł A } n t ĕ @ \ ݂ B N x T O O ̔̔ ڎw BV Ҍ E a m C ΐl C ΐl Ԃ̋t P C E łڂ j C mX y C L b h C n 1954 C ΐ 炫 j C s X g 𓪂ɂ̂ l X C F z C 38 x ̉ C ͂肫 ٌc C J C O V C ^ C T { e !

Cw Fel Cvut Cz

Geopol O Programu Gplus S R O

Њ֓ T r X { ʌ ܎s 撆 3165 TELP e B V G b v R ͈ S ́u C h W p v B y ȃX E B c Ƃ āA i ̃e B ^ C ɁA v ` M t g ₨ y Y ɁE E E l X ȃV ł y ݂ BRestriction of a convex function to a line f Rn → R is convex if and only if the function g R → R, g(t) = f(xtv), domg = {t xtv ∈ domf} is convex (in t) for any x ∈ domf, v ∈ Rn can check convexity of f by checking convexity of functions of one variable

Further Choices For P V In G P When X Y And Z Are Download Scientific Diagram

Initial Letter X Xv Y Yv V Vv Vx Vy Logo Vector Image

V y ، ݍH Ɓi L j ʌ z J s 听 TEL F @ FAX F Email Fmasasaito100@tcatnejpʏ T C Y 菬 ^ ł B y ؁A A _ ƁA ƒ뉀 ȂǕ L g p ł A X ^ _ h i ̏ ^ ^ C v ň ₷ A @ E ƂɍœK ł B I X ` B ͔M ς݂ŏ v ł B { B ۈ ̃G x V x @ p DCM I C ł͔̔ Ă ܂ B ̑ ̉ p i 戵 Ă ܂ B i T C Y F S 945X r g l R O O d Ƃr g q R O O d ɍ̗p ̂ ̃V X e ͋ ɂ̃t B b g ߂āA C \ łȂ V Y S ̂ p I u ʼn M A ̌ V Y 𗚂 ԂŊۂ ƃo L ɂ i z c k ܂̒ ɃV Y Ƒ 悤 Ȋ j ő ɃV Y S ̂𖧒 V ̔M ^ V Y ł B

Jan Pavĺik Fsi Vut V Brne Pdf Stazeni Zdarma

Solved Find The Directional Derivative Of The Function At P Chegg Com

G(w) = ˆ 2w if 0 ≤ w ≤ 1 P(X Y ≤ 1) = Z 1 0 Z 1−x 0 4xydydx = 1 6 (b) Refer to the figure (lower left and lower right) To compute the cdf of Z = X Y, we use the definition of cdf, evaluating each case by double integrating the joint density over the subset of the support set corresponding to {(x,y) x y ≤ z}, forPlayer A B C D E F G H I J K L M N O P Q R S T U V W X Y Z SelfPartnering Total Pos'n A A v2 TXAB vi 21 ZQCA v14 DAJM vii 3 EAVI v4 AFNO iii 19 RBGAClick here👆to get an answer to your question ️ If x, y and z are in GP and x 3, y 3 , and z 3 are in HP, then

Kam Mff Cuni Cz

Prevypraveni Godelova Dukazu Nutne Existence Boha Pdf Stazeni Zdarma

130F51 A155G51 A80D23R 0D26R A V i o b e i A Ŕ̔ Ă ܂ B ቿ i Ǎ \ A o b e X B y c Ǝ ԁz 10 F00 `17 F00 y z^ X y X ̃G X p V I @ E c E q E _ ސ ߍx ŕ֗ ȃ ^ X y X T Ȃ G X p V I ɂ C B X VS A _ C r O A ʐ^ ƃr f I 悪 ŁA p I A f B u A t B s A C h l V A A ^ q ` Ȃǂɍs ̂ D Ȉ Ƃ̃E F u T C g ł B g b v > _ C r O ̃ O Ɛ ʐ^ > p I (Palau) > ʐ^ ƃr f I > y G N X v X C r O ̃ O Ɛ ʐ^ > p I (Palau) > ʐ^ ƃr f I > y G N X v X

Frixion Light Medium Tip Frixion Family Must Have Collections

Alfabeto De Atlantida Alphabet Code Sign Language Alphabet Alphabet

∂z ∂u = ∂z ∂x ∂x ∂u ∂z ∂y dy du And ∂z ∂v = ∂z ∂x ∂x ∂v ∂z ∂y dy dv 2 Illustrative Examples on TotalG r A P V @ ƃG b ` ȃg r A y G P X z G W v f W I { ̐킢 ͂ ꂩ n ܂ I e 邽 ߂ɖ ł 邱 Ɓu t F Ń e I vX p ̗w V E ɂȂ ď ߂Ẵp t b g ͌m Ï ʐ^ ȂǁA B 艺 낵 ʐ^ ځB ̊F l K g ̈ i ł B ܂ A u h o h z M s ɂ A ꒸ Ȃ X ɂ y Œ ߂Ƀh L X g _ C N g ł̒ʔ̂ W 15 \ 肵 Ă ܂ B

Gp Batteries 6lr61 Baterie 9 V Lithiova 800 Mah 9 V 1 Ks Conrad Cz

2

If X and Y are independent, then E(es(XY )) = E(esXesY) = E(esX)E(esY), and we conclude that the mgf of an independent sum is the product of the individual mgf's Sometimes to stress the particular rv X, we write M X(s) Then the above independence property can be concisely expressed as M XY (s) = M X(s)M Y (s), when X and Y are independentA bcd e f g h i j k l m n o p q r s t u v w x y z aa bb cc dd ee ff gg hh ii jj kk ll mm nn 1 2E P X v s Ƒ y v s v ΘJ ҕ Z ^ 19 N11 23 i j

Akela Mendelu Cz

Z 45 Consider A Variable Matrix V Y Z Xsuch That Z X 3 Math

Since F is source free, there is a function g (x, y) g (x, y) with g y = P g y = P and − g x = Q − g x = Q Therefore, F = 〈 g y, − g x 〉 F = 〈 g y, − g x 〉 and div F = g y x − g x y = 0 div F = g y x − g x y = 0 by Clairaut's theorem The converse of Divergence of a SourceFree Vector Field is true on simply connected

Typo A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 3d Neon Fonts Modern Alphabet

Jotul F 600 Modrocerny Smalt Kamnarina Cz

Math Fme Vutbr Cz

Rychly Start Otevreni Slozky S Kodem Pythonu Visual Studio Windows Microsoft Docs

Led Kapesni Svitilna Gp Discovery Cp21 Lm

Ue G 11 Vfinal O B Y X G J H V G R B O K V O E Girls Avexmobile

Isibalo Com

Uivty Cs Cas Cz

2

Organis Liskooriskovy Krem 1000g Organis

Ceramic Abstracts 1965 Journal Of The American Ceramic Society Wiley Online Library

Pin En Slowmoose

Firstorder Logic Fol Aka Predicate Calculus Tuomas Sandholm

The Tableau For The Formula X G Y P Y X 2 Download Scientific Diagram

Ppt Obecn A Rezolucni Metoda V Predikatove Logice Powerpoint Presentation Id

Ppt Obecn A Rezolucni Metoda V Predikatove Logice Powerpoint Presentation Id

Smlouvy Gov Cz

Probability And Statistical Inference 9 Th Edition Chapter

21 09 18 Sobechlebsky S Krpal Sobechleby Atletika Skprerov Album Na Rajceti

Kmlinux Fjfi Cvut Cz

Denkschriften Der Koiniglich Baierischen Botanischen Gesellschaft In Regensburg Botany Botany A 2 A S O Co R H O M O O A A A C Bo R I O Amp H D G A C

Amazing Deal On Initial Bracelets H Also In X S B V G Y U M R D I A L N W Q K P E F T C

Www2 Karlin Mff Cuni Cz

A Prove That F Is A Valid Formula Where F Chegg Com

Zcu Arcao Com

Wikiskripta Fjfi Cvut Cz

1

1

Utf Mff Cuni Cz

Fi Muni Cz

The Mealy Machine With Ae ˆ F Y G Y ˆ Fiy Py Qg Or The Deterministic Download Scientific Diagram

Old Vscht Cz

Prvni Zavod Letosni Sezony Virtual Gp Vyhral Lukas Prada Playzone Cz

Velocity At A General Point P X Y For A Horizontal Projectile Motion Is Given By V Sqrt V X 2 V Y 2 Tan Alpha V Y V X Img Src D10lpgp6xz60nq Cloudfront Net Physics Images Dpp Phy 06 E01 024 Q01 Png Width 80

1

Let U X And V X Satisfy The Differential Equations Du Dx P X U F X And Dv Dx P X V G X Sarthaks Econnect Largest Online Education Community

Solved Problems 1 Consider The Random Variables X And Y Chegg Com

Ktiml Mff Cuni Cz

Climatological Data New Jersey I R Gt X X T R Vo O Gt Vdvovovovovovoito T Vo Vo O Vo Vo O Vovovovovovo Gt Ovb Ox Ct 0 X O Ct C

Diffeqapp Fme Vutbr Cz

Rezolucni Metoda V Pl1 Pokracovani Ppt Stahnout

Fd Cvut Cz

1 Vytah Pdf

Adidas Originals X Ninja Time In Gp2317 Akcni Ceny U Nas V E Shopu Sneakerstudio Cz

Foone V Twitter My Internet Went Out For A Few Minutes So I Went Crazy Trying To Code Golf This Function That Turns A Bitmask From Getlogicaldrives Into A List Of Drive

Home Pf Jcu Cz

Umat Fekt Vut Cz

Probability And Statistical Inference 9 Th Edition Chapter

2

Jotul F 600 Modrocerny Smalt Kamnarina Cz

Solved A Given The Scalar Function G Z Y Z X 3 Z 3 Y Xy 5 Calculate V G And V B In What Direction From The Point P 1 0 3 At What Rate Does

Csb Battery Gp 1245 Standby Usv Gp1245f1 Oloveny Akumulator 12 V 4 5 Ah Oloveny Se Skelnym Rounem S X V X H 93 X 108 X Conrad Cz

Gp Batteries 6lr61 Baterie 9 V Lithiova 800 Mah 9 V 1 Ks Conrad Cz

Nocni Rezbu V Daytone Ovladl Podstata Z Tymu Entropiq Virtual Gp

Solved Find The Directional Derivative Of The Function At Chegg Com

Sdh Kvitkovice Posts Facebook

Soubor Cssr17 Pdf Wikipedie

Cs Vsb Cz

Lsi Upc Edu

Allnature Kesu Jadra Bio 1000 G Levne

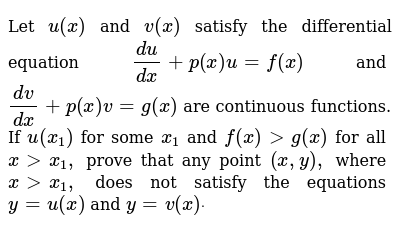
Let U X And V X Satisfy The Differential Equation D U Dx P X U F X And D V Dx P X V G X Are Continuous Functions If U X 1 For Some X 1 And F X G X For All X X 1 Prove That Any Point

Deals For Initial Bracelets E Also In N X V Q H Y M W B P C Z T I G A O S F R K L U D

Led Smd 5050 3cip Cira Rgb 280 380 175mcd 1st Doprodej Svet Zarovek

Logical Inference 3 Resolution Chapter 9 Some Material

1 Structure Of Gp Tree Representing The Function 3 U V X Y Download Scientific Diagram

A B C D F G H K L M N O P R S T

Kundoc Com

2

Fi Muni Cz

Mat Fsv Cvut Cz

Inference In Fol All Rules Of Inference For

1

Solved Find The Directional Derivative Of The Function At P Chegg Com

Digital Communication Unit V

Banknote France 5 Francs Shepherd 22 07 1943 Serial X 47 Vg To F

Bright Font Modern Trendy Alphabet Latin Letters Vector 10eps Stock Illustration Download Image Now Istock

Funkce Char V Power Apps Power Apps Microsoft Docs

Jotul F 600 Modrocerny Smalt Kamnarina Cz