[コンプリート！] 三角 錐 体積 求め 方 203071

 三角柱の体積の求め方は 「底面積 × 高さ」でしたね。 底面積は 4 × 4 × 1 2 = 8 よって、三角柱の体積は 8 × 8 = 64 体積は 64（ c m 3 ） となります。 続いて、 三角柱の表面積の公式は 「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた 8 c m 2 三角錐 次は下の図のような三角錐の体積 を求めてみたいと思います。 まず積分する方向を今回は 軸方向と決めたいと思います。 よって は0から1の範囲で積分することになります。 また、この三角錐は 平面と平行に切り取った薄い三角形がたくさん集まったものと考えることができます。 ここまでは円柱の体積と同じだったのですが、三角錐で違うところが が下の図によって三角錐の体積の求め方を考えます。 上の図のように縦横高さが等しい立方体を半分に切った三角柱を考えると、 この三角柱は、上図のように、体積が等しい（底面積が等しく高さが元の立方体の辺の長さの）3つの三角錐に切り分けることができます。 それで、三角錐の

簡単公式 三角錐の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

三角 錐 体積 求め 方

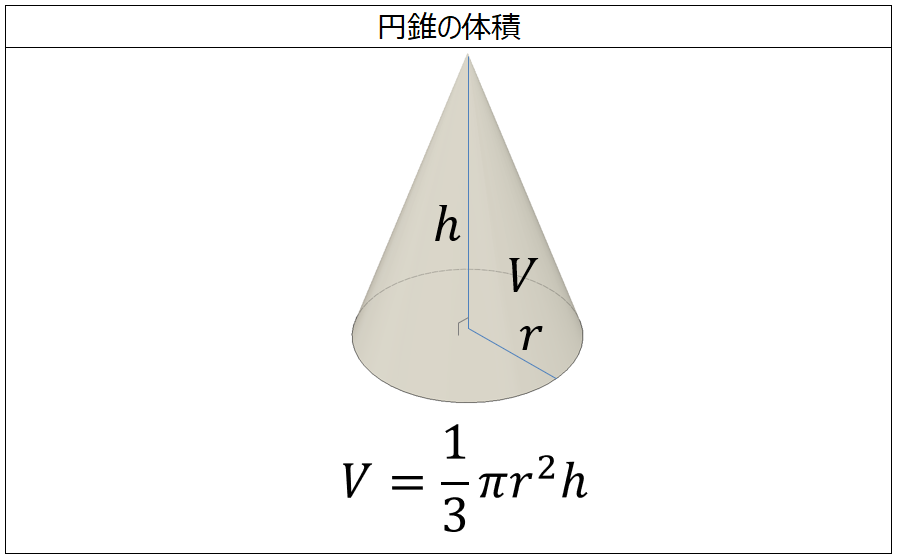
三角 錐 体積 求め 方-このように、三角錐の体積は、底面積×高さ÷3を計算してもらうと求めることができます。 4．四角錐の体積の計算 下の図が 四角錐 の立体図形です。要点四角錐，三角錐，円錐の体積 三角錐，四角錐，円錐の体積 V は，それがちょうど入る四角柱，三角柱，円柱の体積の です． 特に，円錐については，底面の半径が r であるとき，底面積が S=πr 2 と書けるから と書くこともできます．

円錐の体積ってなんであの公式なの Webty Staff Blog

 だから、三角錐の体積を求めるときも「1/3」をかけるんだ^^ まとめ：円錐の体積の求め方の公式はシンプル 円錐の体積の求め方はどうだったかな？？ 底面積×高さ×1/3 という公式は意外とシンプルだったよね笑上の図は底面が円なので円錐、底面が三角形だったら三角錐、底面が五角形だったら五角錐、底面が百八角形だったら百八角錐と呼ばれます。 柱と錐の体積 どちらも公式は簡単です。 柱の体積＝底面の面積×高さ 錐の体積＝底面の面積×高さ÷3 この記事の目的：錐形を求める際に「3分の1」する理由を中学生にも分かるように説明する． はじめに 錐形は3分の1 指針 ①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積が変わると？ 最後に

四角錐や五角錐の体積の求め方 忘れている人が割といるので確認しておきます。 柱体と錐体の体積の求め方です。 \(\,\color{red}{(柱体の体積)=(底面積)\times (高さ)}\,\) です。 これは、底面の形に関係なく同じです。 三角柱でも四角柱でも円柱でも同じ。三辺の長さが a, b, h の 直方体(ちょくほうたい) 三辺の長さが a,b,h a, b, h の直方体の体積 V V は、次の式で求められます。 直方体 ( ちょくほうたい ) の体積 V = abh V = a b h 体積 = たて × 横 × 高さ 12三角錐の体積公式 錐の体積 底面積×高さ× (1/3) 三角錐に限らず、錐の体積を求めるには柱との関係で捉えるとよいでしょう。 つまり、柱の体積に3分の1をかければ、錐の体積が求まるという関係にあります。 そして、これを三角錐に関して表現すると、 三角錐の体積 底面積（三角形の面積）×高さ× (1/3) このように表現されることになります。

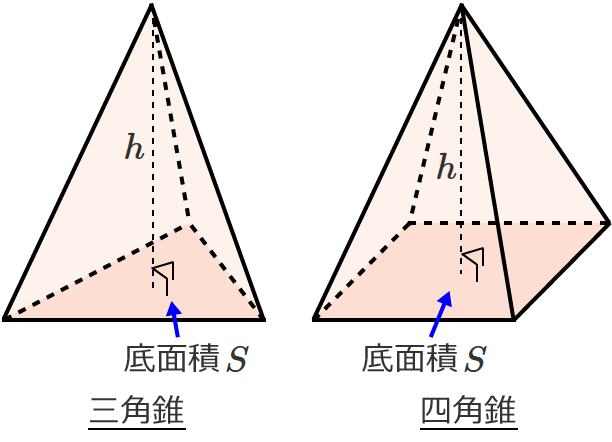
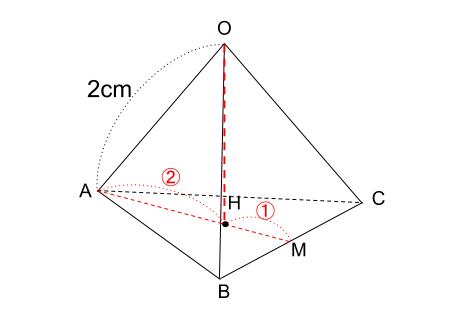
以下に、三角錐の重心の性質の簡単な求め方を示します。 上の図のように、三角錐の重心を3次元座標の原点Oにして考えます。 三角錐ABCDの頂点の座標の平均 （A＋B＋C＋D）／4 が三角錐の重心です。 図のように、A＋B＋C＋D＝（0，0，0）となるように座標を定めます。 ここで、三角錐の底面の三角形BCDの重心Gを定めると、 Gの座標は、 G（（bcd）／3，（efg）／3等辺三角形になることがわかるので， 三角錐AOEF ＝3×3× 1 2 ×6× 1 3 ＝9 cm3 となります。 三角錐OAEF＝三角錐AOEF より，求める体積は9cm3 (3)体積を表す式から高さを求める (2)より，三角錐OAEF＝9cm3 と求められているので， 底面の三角形の面積が \(S\)、高さが \(h\) の三角錐の体積 \(V\) は、次の式で求められる。 \begin{align}\color{red}{V = \displaystyle \frac{1}{3}Sh}\end{align} (体積) = \(\displaystyle \frac{1}{3}\) × (底面積) × (高さ)

簡単公式 三角錐の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

三角錐の体積と表面積の求め方 計算プロセスがよくわかる図形のイラスト付き

円錐の体積の求め方 公式と計算例 Scipursuit 体積の求め方 円錐 円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の 今回は、三角柱の体積の求め方公式について書いていきたいと思います。 // 三角柱の体積の求め方公式 三角柱の体積を求める問題 問題① 《三角柱の体積の求め方》 問題② 《三角柱の体積の求め方》 問題③ 《三角柱の高さの求め方》 問題④ 《三角柱の高さの求め方》 三角柱の体積 どうして1/3なの？錐の体積の公式の求め方 突然ですがみなさん、錐の体積の求め方はご存知ですか？ 体積＝底面積×高さ×1/3 ですよね。こちらは中学1年生で習う公式です。 教科書でこの公式を知ったとき、授業でこの公式を習ったとき、

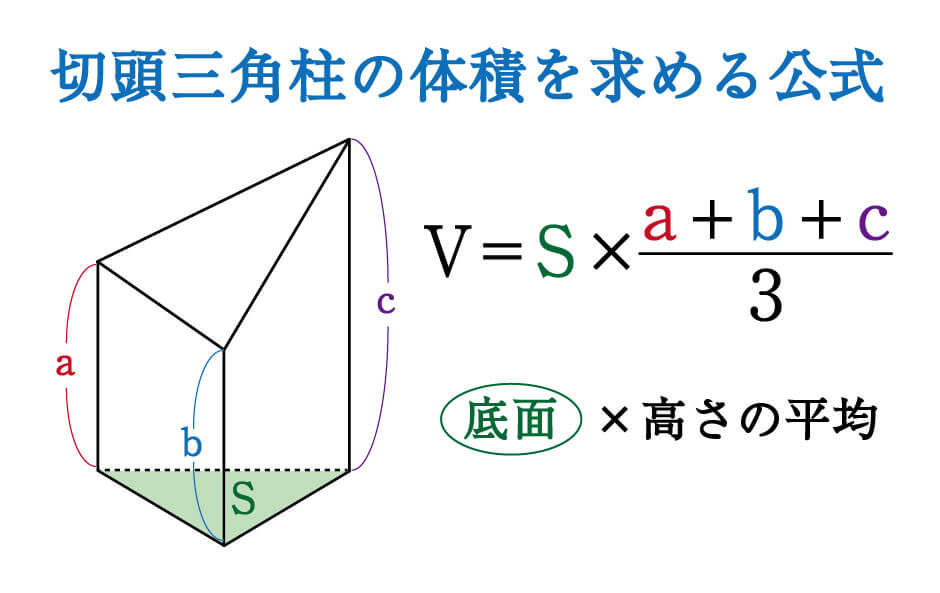
数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三角柱の体積を求める時にテキストでは2分の1と出ているんですがこれは何なんで Yahoo 知恵袋

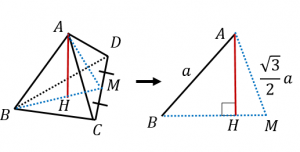
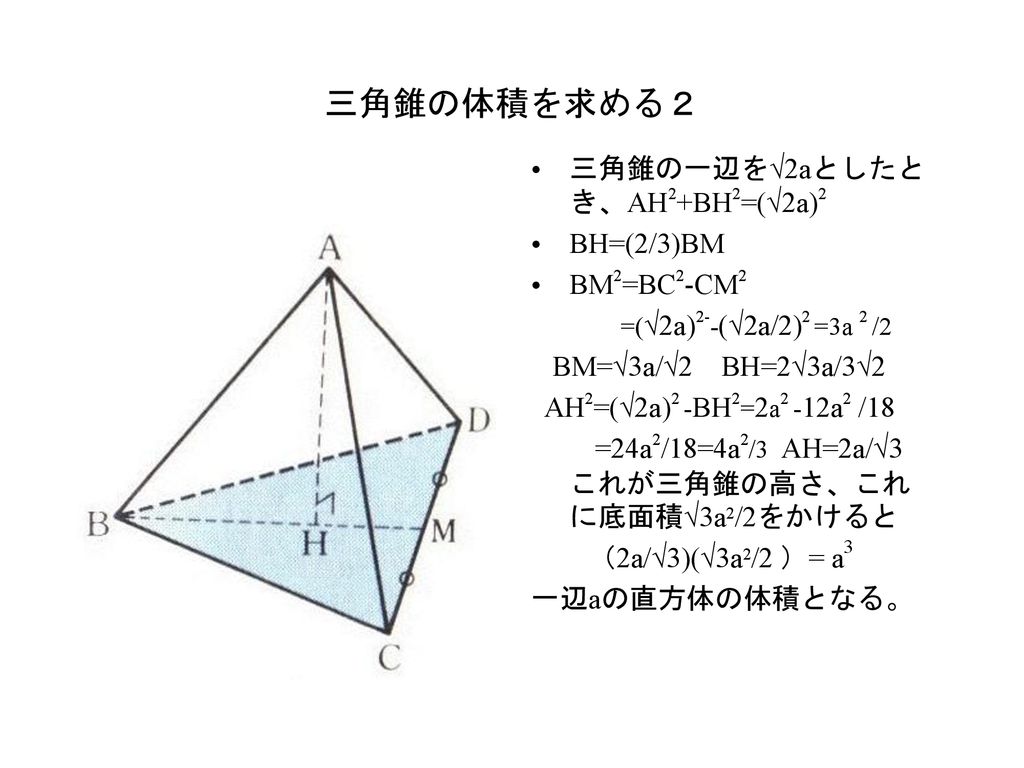
 今回は、四角錐（しかくすい）の体積の求め方（公式）について書いていきたいと思います。 四角錐の体積の求め方公式 四角錐の体積を求める問題 問題① 《四角錐の体積の求め方》 問題② 《四角錐の体積の求め方》 問題③ 《四角錐の高さの求め方》 (adsbygoogle = windowadsbygoogle三角錐の体積は、三角柱の体積を1/3にすればよいです。 三角形の底辺が3、高さ4、三角錐の高さが5のとき 三角錐の体積＝3×4÷2×5÷3＝10cm 3ようやく体積を求める準備が整いました。 この正四面体の高さ OH O H は下図のようになっています。 OH O H が何 cm c m なのか求めます。 当然、三角形 OAH O A H に三平方の定理を用います。 AM A M は 1 1 辺が 2cm 2 c m の正三角形の高さなので、 AM = √3cm A M = 3 c

一辺が12cmの立方体の中にある三角錐の体積の求め方を教えてく Yahoo 知恵袋

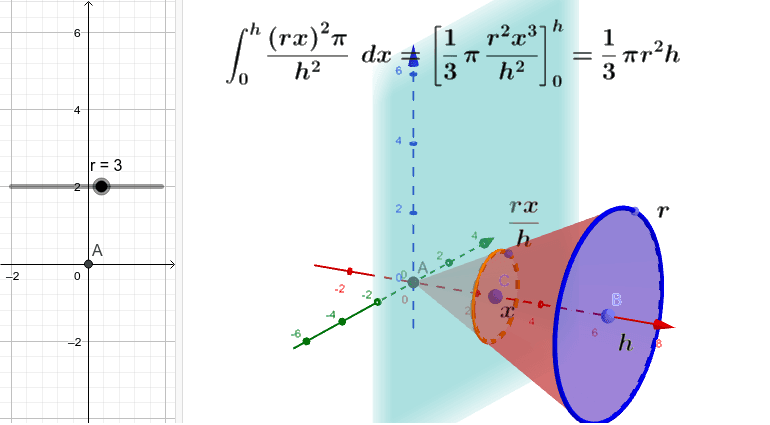
円錐の体積の求め方 Geogebra

 三角柱の体積の求め方（公式） では最初に簡単な 三角柱の体積の求め方 から解説していきましょう！ 求め方はとても単純で、 「底面積\(×\)高さ」 で体積は求められます。（2）この三角錐を、\(3\) 点 \(p,q,r\) を通る平面で切断したとき、点 \(o\) を含む立体の体積は、もとの三角錐の体積の何倍か求めなさい。 解説 （1）も（2）も、重要な図形のテクニックが学習できる良 三角錐，四角錐，円錐，の錐 (すい)という漢字は訓読みでは「きり」と読みます．これは，小さな穴を開けるための先のとがった工具です． 三角錐や円錐といった「錐」とは，穴をあける道具のように先の尖った立体です． では，「〇〇錐」の体積の求め方はどうだったかというと， (〇〇錐の体積) = (底面積)× (高さ)× 1 3 ( 〇〇錐の体積) = ( 底面積) ×

空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト

立体の体積 無料で使える中学学習プリント

三角錐の体積＝底面積 高さ 三角錐の体積を求めるときに気をつけたいのは、 必ず を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず を掛けてください。 また、底面の三角形の面積は、 底面 高さ となることもおさえておきましょう。 すると、計算は次のようになります。 〇 三角錐の体積は、底面積を求めて高 立方体の中にある三角すい たくさんの中学で出題されている問題です。 高さが2cmの二等辺三角形4つを切り取ってできたものです。 これを組み立ててできる四角すいの体積を求めなさい。 ただし、角すいの体積は、 (底面積)× (高さ)÷3で求められます。 底面積は正方形の対角線がわかるのですぐ求められます。 こんな↓展開図になります。 では組み立て三角錐の体積 三角錐の体積＝底面積×高さ× 1 3 証明 三角柱を3つの三角錐に分解することで証明する． (Ⅰ)三角錐 eafc と三角錐 eafd について 三角柱 abcdef の側面 acfd は平行四辺形である． よって

立体の体積を求める公式

Mathematics 錐体の一部の体積 働きアリ

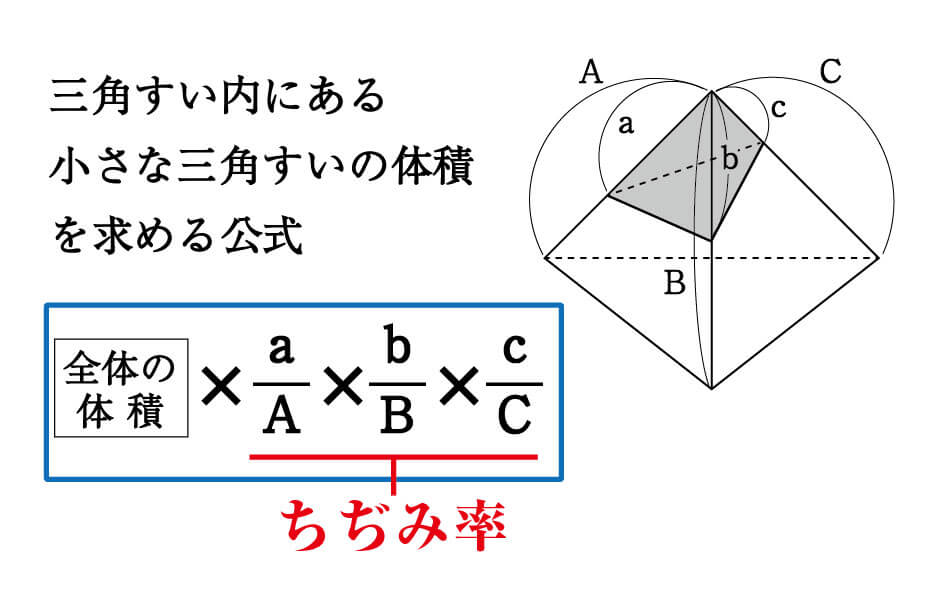
三角すいの内部で、一方向へ縮んだ三角すいの体積は、以下の公式で求めることができます。 全体の体積に、 、 、 をかけたものが、小さい三角すいの体積です。 この 、 、 をかけ合わせた分数が、本講義で"ちぢみ率"と呼んでいるもの。 ちぢみ率は、元の三角すいに対してどれくらい縮小したのかを表す分数なので、そのまま例題の答えになります。 実際に 三角錐の体積の求め方 三角錐oabcについて、 OA＝OB＝OC＝5 AB＝4 BC＝5 AC＝6 この三角錐の体積の求め方を教えていただけませんか？？ 底面積は出せるのですが、高さの出し方がどうしてもわかりません。 宜しくお願いします。 ＊グラフ上の三角形の面積の求め方は、記事内の「座標の指導案（応用）」の章で解説しています。 練習問題 では錐の体積の練習問題です。 問題3は長崎県の公立高校入試問題。19年度の大問4の13をそのまま載せます。

円すい 円錐 の体積の求め方と問題 小学数学 Irohabook

3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ

1

三角錐 四面体 の体積の公式 Schoolmath S Diary

コンプリート 三角錐 体積 求め方 シモネタ

Studydoctor相似比と体積の計算 円錐台 三角錐台 中学３年数学 Studydoctor

3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ

中学数学 三角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく

簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ

正四面体の高さと体積の求め方 具体例で学ぶ数学

数学の問題教えてください 立方体から切り取った三角錐の体積はどうやって Yahoo 知恵袋

三角錐の体積の求め方 三角錐o Abcについて ｏａ ｏｂ ｏｃ ５ Okwave

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

三角錐の体積の公式は 1分でわかる公式 問題 底面積との関係

中学数学 三角柱の体積の求め方と公式 5秒でわかる なぜか分かる はかせちゃんの怪しい研究室

毎日問題を解こう 27 苦手な数学を簡単に

この三角錐の体積とその求め方を教えてください よろしくお願いします Clearnote

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

角錐の体積の公式は 1分でわかる公式 柱体の体積との違い 3分の1になる証明

中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室

角錐 円錐の体積と表面積の公式 数学fun

高校数学 対称面をもつ四面体の体積 受験の月

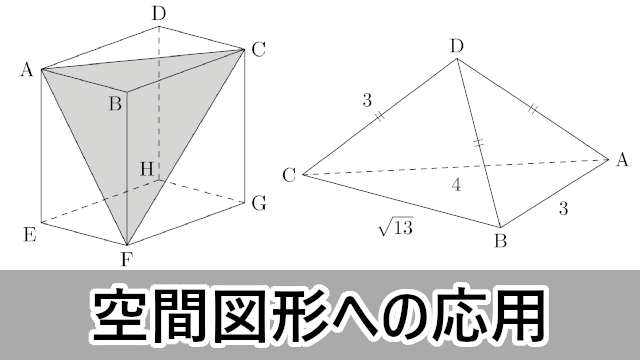
数学ia 空間図形の応用問題 広島工業大 東京慈恵会医科大 大学入試数学の考え方と解法

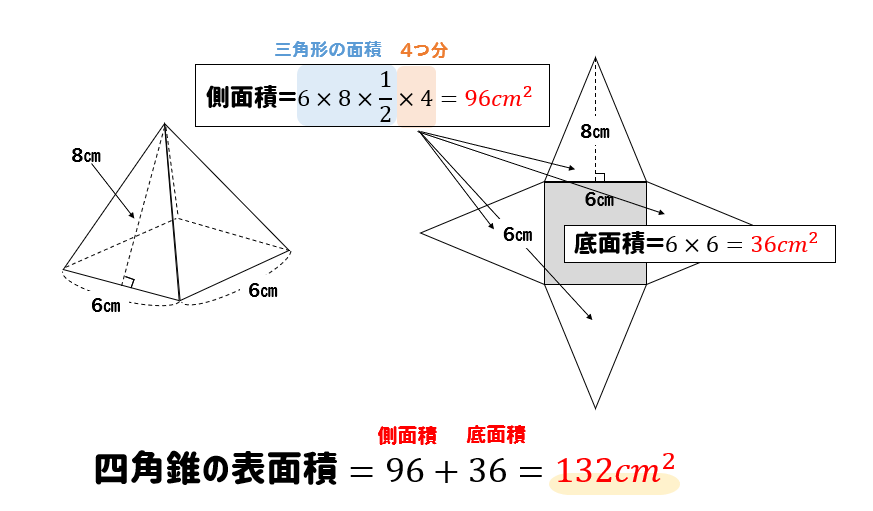
3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ

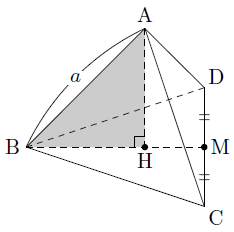
角錐の高さと体積 まなびの学園

3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ

体積の計算 円錐 製品設計知識

６年算数角柱と円柱の体積 立体の体積 教え方

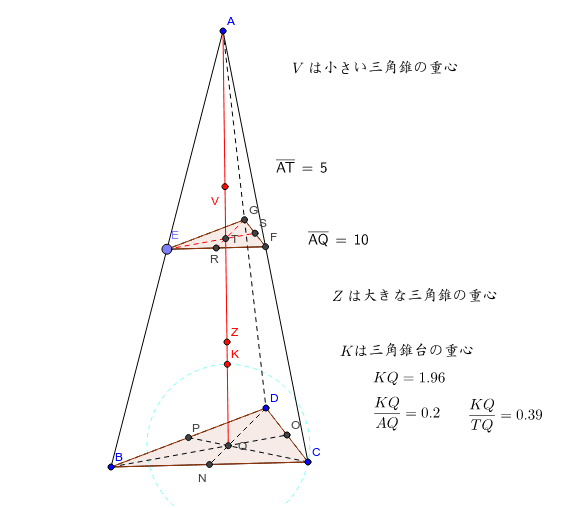
三角錐台の重心 Geogebra

三角錐の体積に関するある私立中学校の入試問題 身勝手な主張

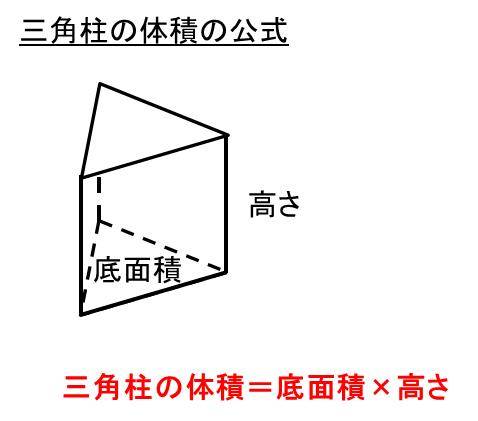
三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム

角錐の体積の求め方 簡単な問題で公式の使い方がわかるよ 中学や高校の数学の計算問題

体積の求め方 計算公式一覧

簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

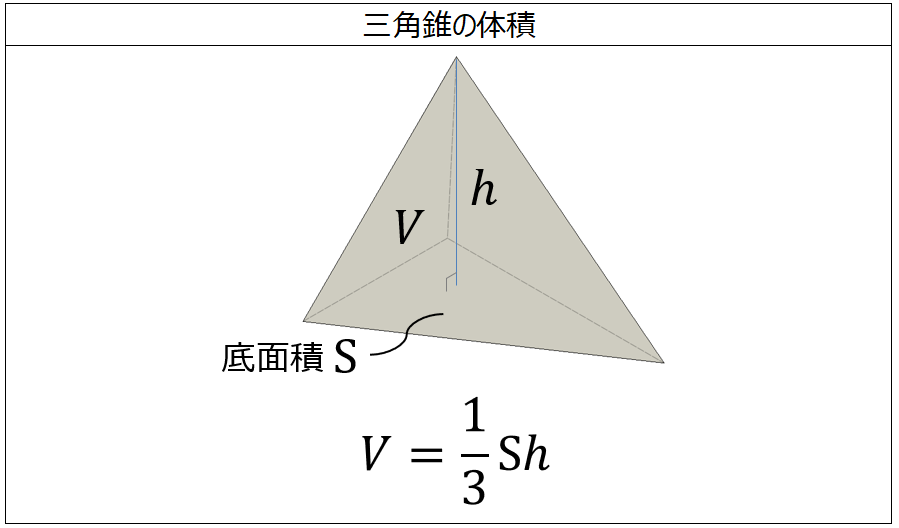
体積の計算 三角錐 製品設計知識

体積計算アプリvolume Calculator Download App For Iphone Steprimo Com

中3 三角形の相似 円錐の体積比 日本語版 Youtube

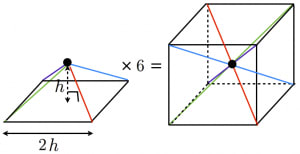
錐体の体積に1 3がつくことの２通りの説明 高校数学の美しい物語

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun

三角錐の体積の求め方 Geogebra

三角錐とは 体積 表面積の公式や求め方 受験辞典

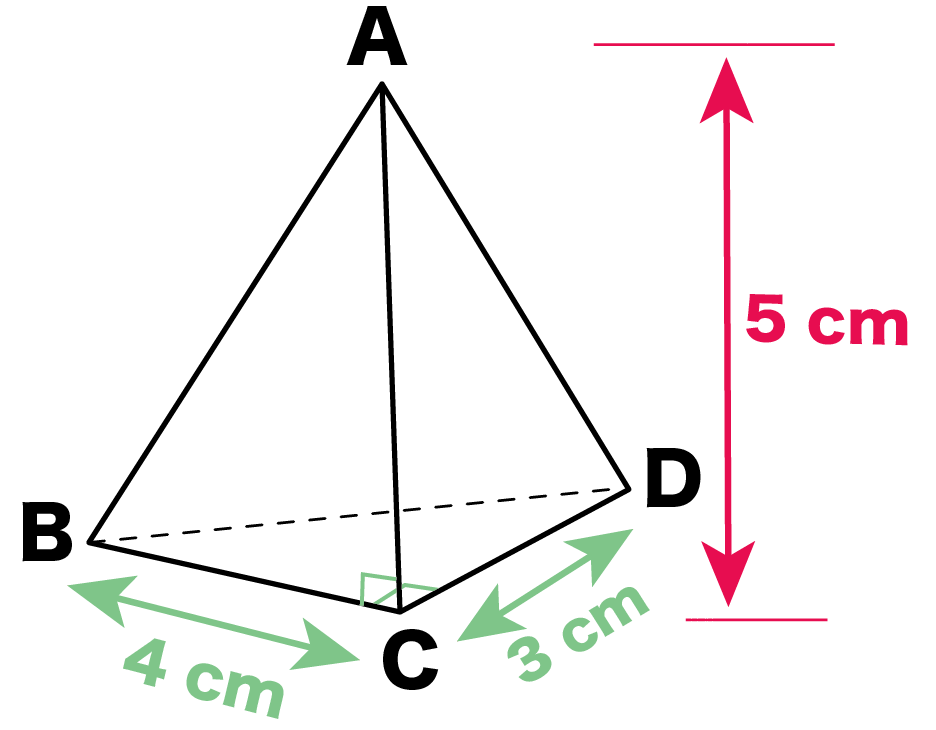
簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題

円錐や三角錐の体積比の求め方 相似比 辺の長さの比から計算 白丸くん

中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室

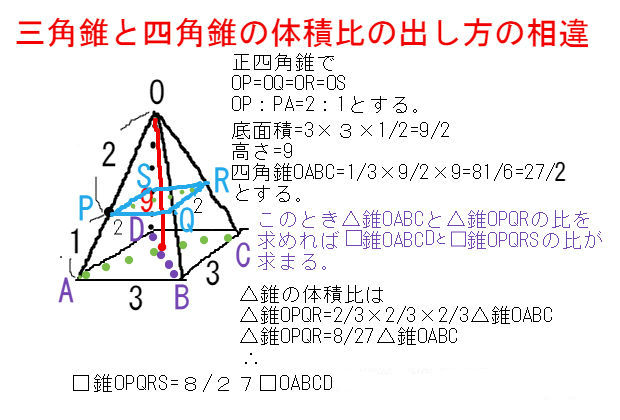
三角錐と四角錐の体積比計算方法の違い 中学 数学 理科の復習サイト

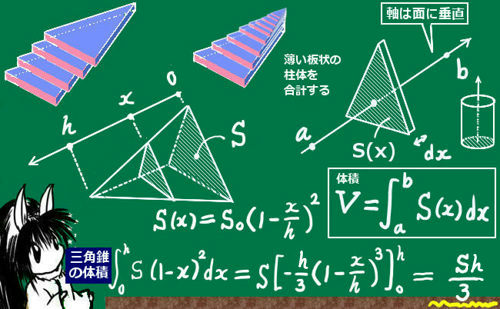
立体の体積計算 積分 高校 理数系無料オンライン学習 Kori

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

2

簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

三角錐の体積の公式は 1分でわかる公式 問題 底面積との関係

1

三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

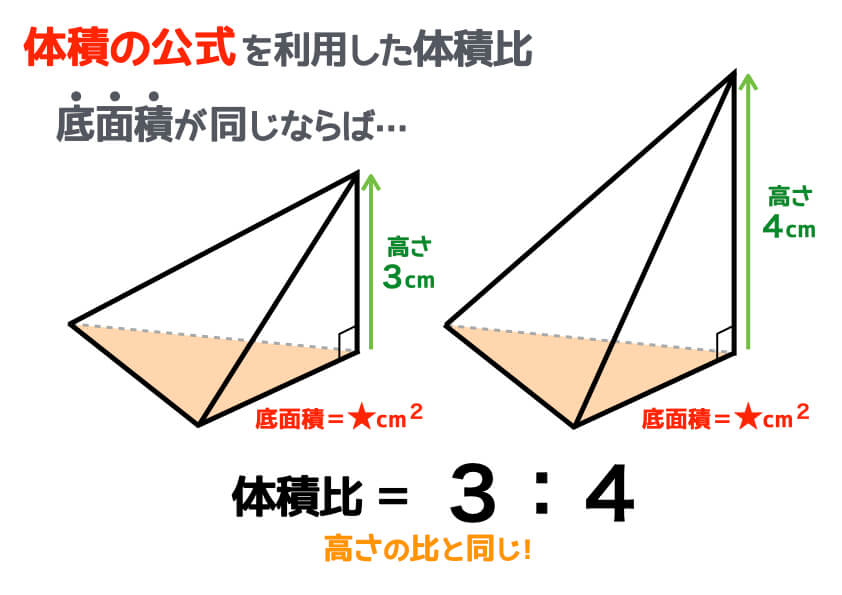
小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ

高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月

三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学

三角錐の体積 積分学まで待たねばならないか Ppt Download

3分でわかる 円錐の体積 表面積の求め方 合格サプリ

三角錐の体積と垂線の長さ Youtube

簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角柱の体積の求め方 公式 小学生 中学生の勉強

3

半径5分の12cm 高さ6cmの双円錐の体積を求めるのに Clearnote

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

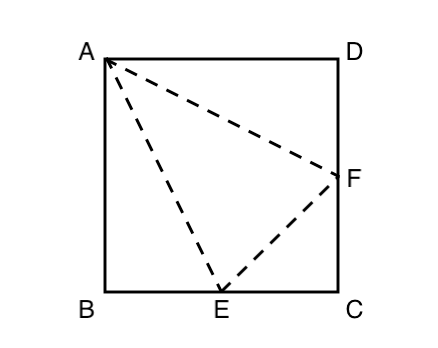
展開図から立体の体積を求める 三角錐の問題 苦手な数学を簡単に

最も人気のある 三角 錐 体積 の 求め 方 ニスヌーピー 壁紙

円錐の体積ってなんであの公式なの Webty Staff Blog

この立体の体積の求め方が分かりません Clearnote

三角柱pの体積は三角錐qの体積の何倍かという問題なのですが 求め方から忘れた Clearnote

三角錐の体積の公式は 1分でわかる公式 問題 底面積との関係

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト

多くの教師が失敗する角柱の体積の求め方 算数を究める

三角錐の体積の求め方 下の図は立方体から三角錐を切り取った立 Yahoo 知恵袋

四角錐の体積の求め方 公式 小学生 中学生の勉強

円錐の体積ってなんであの公式なの Webty Staff Blog

相似比と体積の計算 円錐台 三角錐台 中学３年数学 Youtube

3

正四面体の体積と三角形の重心 中学数学の無料オンライン学習サイトchu Su

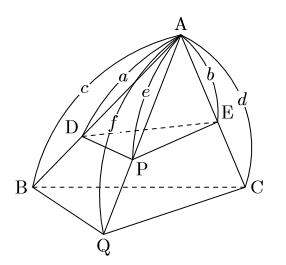
中学数学 公式 三角錐の体積比 数樂管理人のブログ

展開図から三角錐の体積を求める 開智中学 先端ａ改題 09年 算数解法の極意

円錐の体積を求める Youtube

三角柱の体積の求め方 回転体の側面積の考え方 中学１年数学 空間図形

三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ

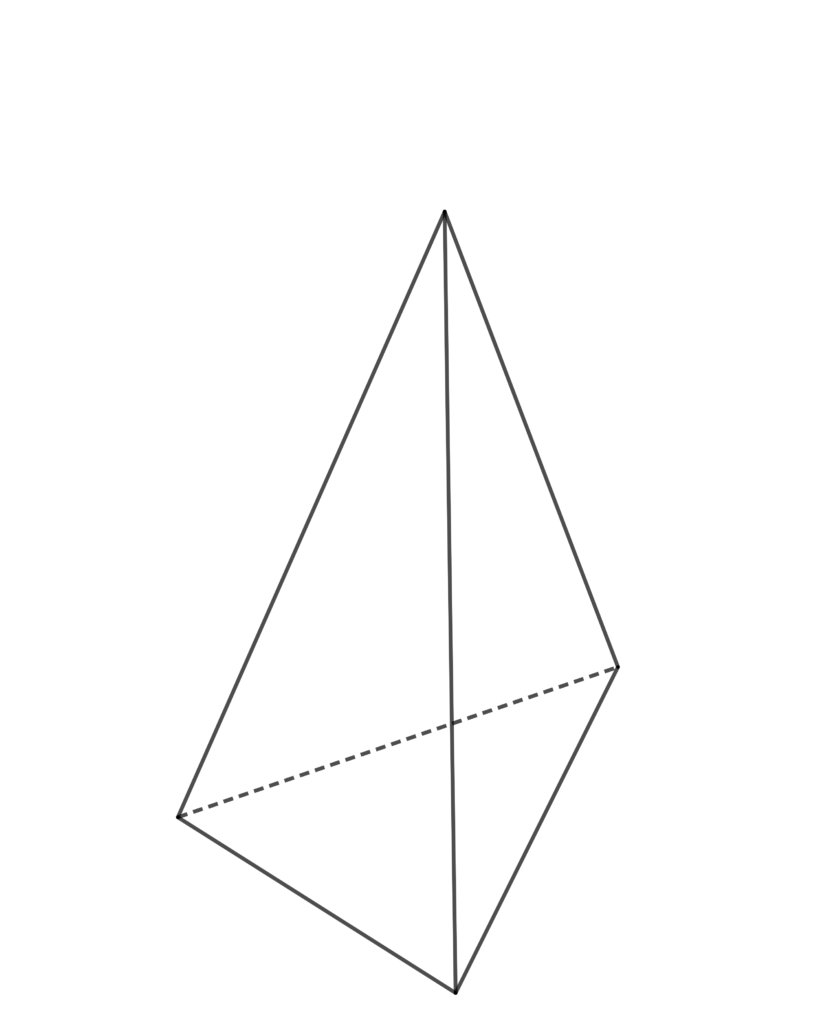
角度を変えて図形を見よう 三角錐の体積の問題 無料高校入試対策問題集 タクマス

体積の求め方 計算公式一覧